Compuertas Lógicas
Las Compuertas Lógicas son circuitos electrónicos conformados internamente por transistores que se encuentran con arreglos especiales con los que otorgan señales de voltaje como resultado o una salida de forma booleana, están obtenidos por operaciones lógicas binarias (suma, multiplicación). También niegan, afirman, incluyen o excluyen según sus propiedades lógicas. Estas compuertas se pueden aplicar en otras áreas de la ciencia como mecánica, hidráulica o neumática.
Existen diferentes tipos de compuertas y algunas de estas son más complejas, con la posibilidad de ser simuladas por compuertas más sencillas. Todas estas tienen tablas de verdad que explican los comportamientos en los resultados que otorga, dependiendo del valor booleano que tenga en cada una de sus entradas.
Trabajan en dos estado, "1" o "0", los cuales pueden asignarse a la lógica positiva o lógica negativa. El estado 1 tiene un valor de 5v como máximo y el estado 0 tiene un valor de 0v como mínimo y existiendo un umbral entre estos dos estados donde el resultado puede variar sin saber con exactitud la salida que nos entregara. Las lógicas se explican a continuación:
- La lógica positiva es aquella que con una señal en alto se acciona, representando un 1 binario y con una señal en bajo se desactiva. representado un 0 binario.
- La lógica negativa proporciona los resultados inversamente, una señal en alto se representa con un 0 binario y una señal en bajo se representa con un 1 binario.
A continuación vamos a analizar las diferentes operaciones lógicas una por una comenzando por la más simple:
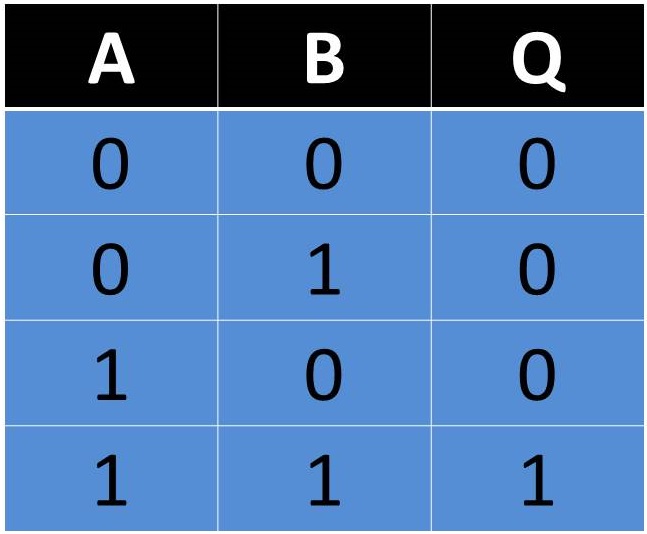
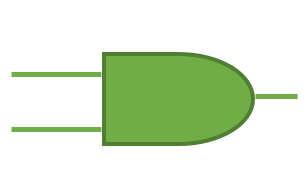
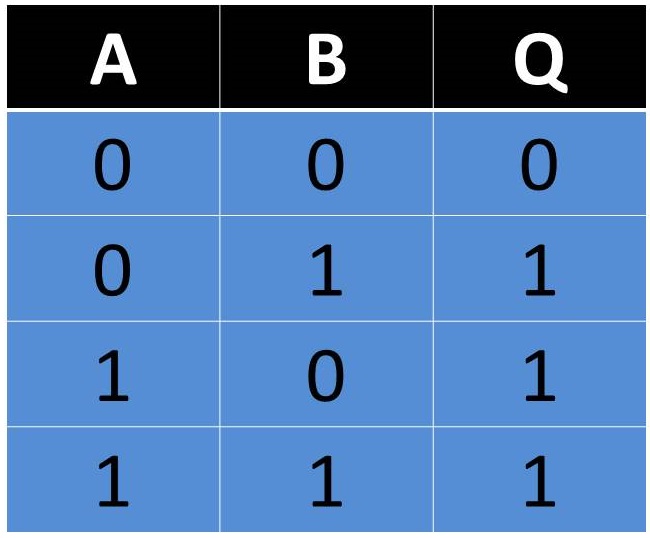
Compuerta AND
Esta compuerta es representada por una multiplicación en el Algebra de Boole. Indica que es necesario que en todas sus entradas se tenga un estado binario 1 para que la salida otorgue un 1 binario. En caso contrario de que falte alguna de sus entradas con este estado o no tenga si quiera una accionada, la salida no podrá cambiar de estado y permanecerá en 0. Esta puede ser simbolizada por dos o más interruptores en serie de los cuales todos deben estar activos para que esta permita el flujo de la corriente.
Fig. 2 Tabla, Representación y Fórmula Compuerta AND
Compuerta OR
En el Algebra de Boole esta es una suma. Esta compuerta permite que con cualquiera de sus entradas que este en estado binario 1, su salida pasara a un estado 1 también. No es necesario que todas sus entradas estén accionadas para conseguir un estado 1 a la salida pero tampoco causa algún inconveniente. Para lograr un estado 0 a la salida, todas sus entradas deben estar en el mismo valor de 0. Se puede interpretar como dos interruptores en paralelo, que sin importar cual se accione, será posible el paso de la corriente.
Fig. 3 Tabla, Representación y Fórmula Compuerta OR
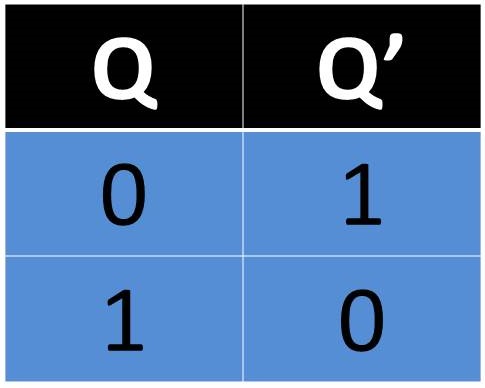
Compuerta NOT
En este caso esta compuerta solo tiene una entrada y una salida y esta actúa como un inversor. Para esta situación en la entrada se colocara un 1 y en la salida otorgara un 0 y en el caso contrario esta recibirá un 0 y mostrara un 1. Por lo cual todo lo que llegue a su entrada, será inverso en su salida.
Fig. 4 Tabla, Representación y Fórmula Compuerta NOT
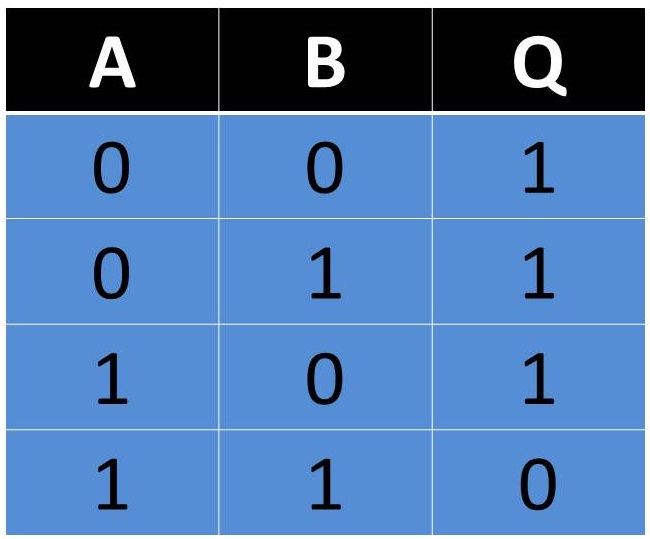
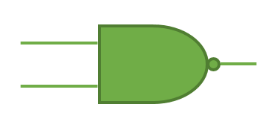
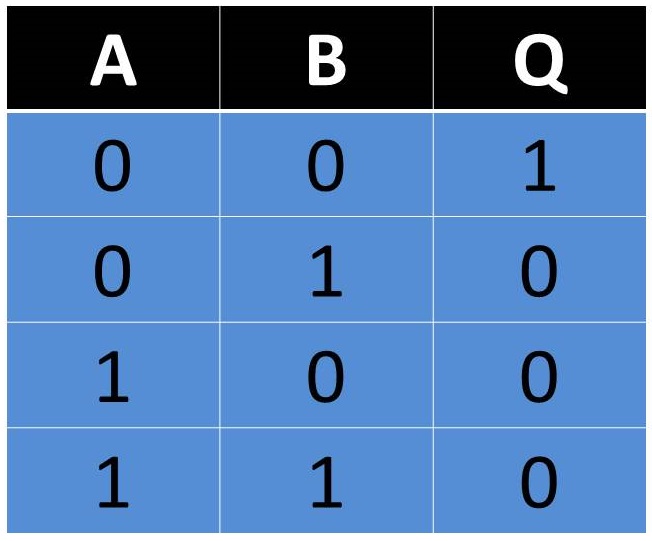
Compuerta NAND
También denominada como AND negada, esta compuerta trabaja al contrario de una AND ya que al no tener entradas en 1 o solamente alguna de ellas, esta concede un 1 en su salida, pero si esta tiene todas sus entradas en 1 la salida se presenta con un 0.
Fig. 5 Tabla, Representación y Fórmula Compuerta NAND
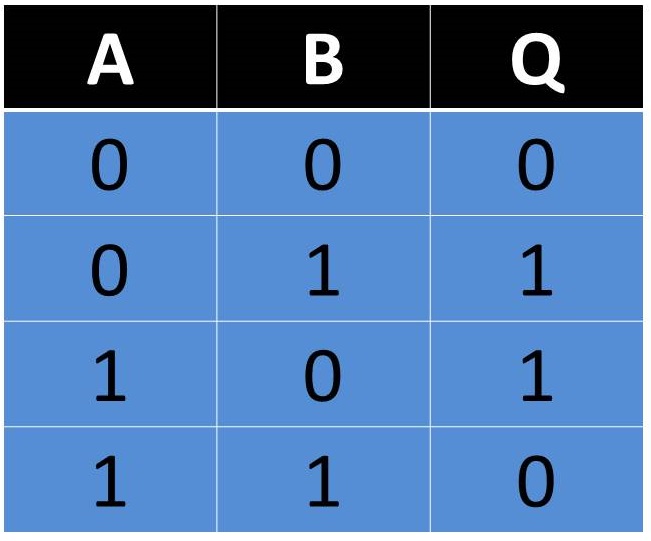
Compuerta NOR
Así como vimos anteriormente, la compuerta OR también tiene su versión inversa. Esta compuerta cuando tiene sus entradas en estado 0 su salida estará en 1, pero si alguna de sus entradas pasa a un estado 1 sin importar en qué posición, su salida será un estado 0.
Fig. 6 Tabla, Representación y Fórmula Compuerta NOR
Compuerta XOR
También llamada OR exclusiva, esta actúa como una suma binaria de un digito cada uno y el resultado de la suma seria la salida. Otra manera de verlo es que con valores de entrada igual el estado de salida es 0 y con valores de entrada diferente, la salida será 1.
Fig. 7 Tabla, Representación y Fórmula Compuerta XOR
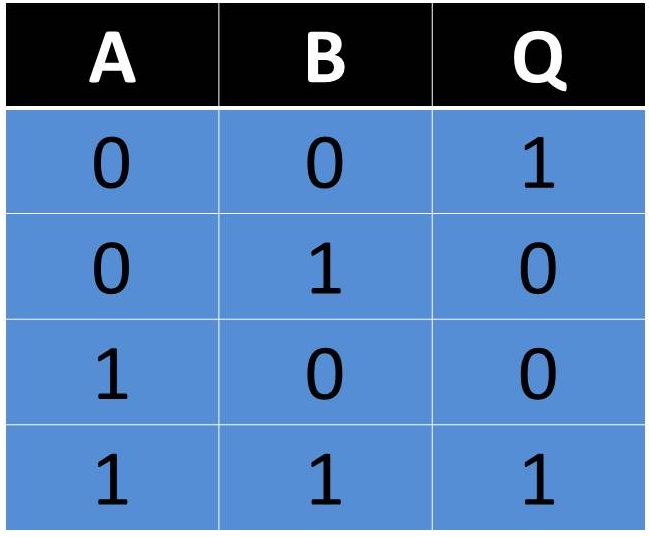
Compuerta XNOR
Esta es todo lo contrario a la compuerta XOR, ya que cuando las entradas sean iguales se presentara una salida en estado 1 y si son diferentes la salida será un estado 0.
Fig. 8 Tabla, Representación y Fórmula Compuerta XNOR
Compuerta IF
Esta compuerta no es una muy utilizada o reconocida ya que su funcionamiento en estados lógicos es parecido a si solo hubiera un cable conectado porque exactamente lo que se le coloque en la entrada, se encontrara en la salida. Pero también es conocido como un buffer, en la práctica se utiliza como amplificador de corriente o como seguidor de tensión para adaptar impedancias.
Fig. 9 Tabla, Representación y Fórmula Compuerta IF
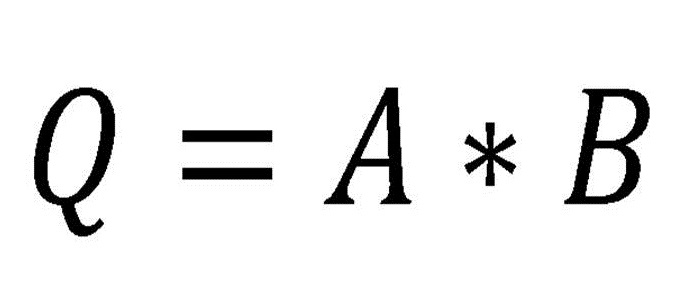


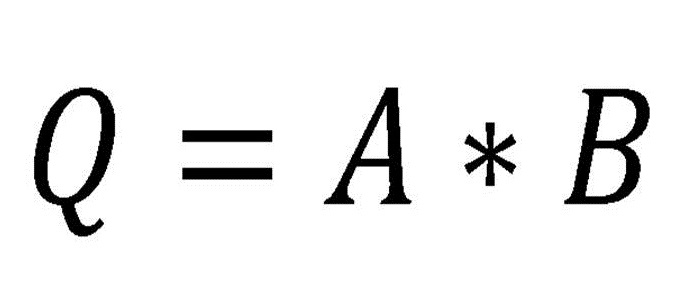

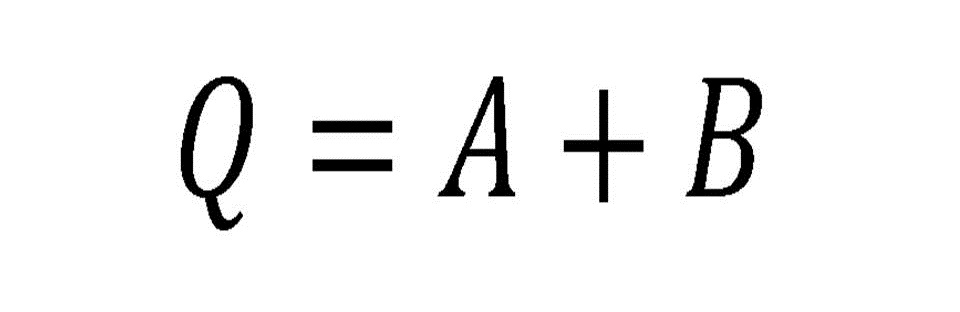


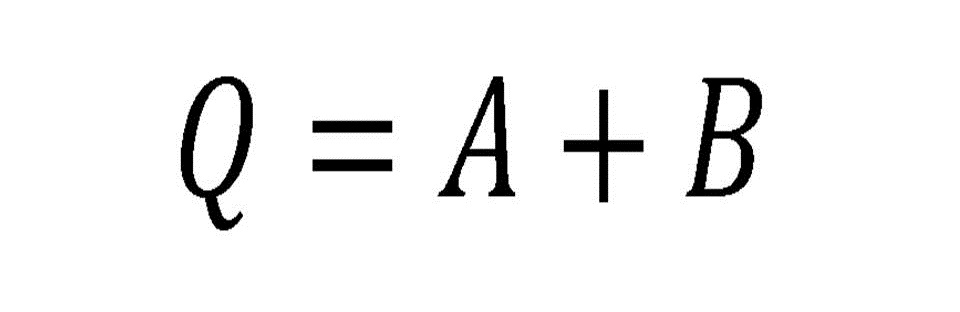

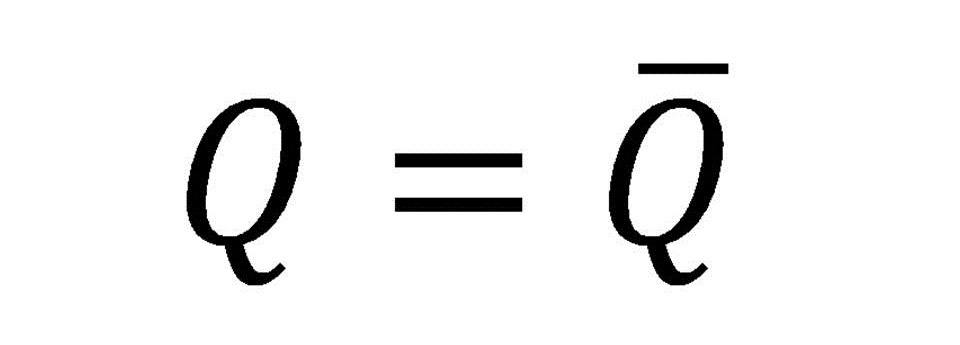


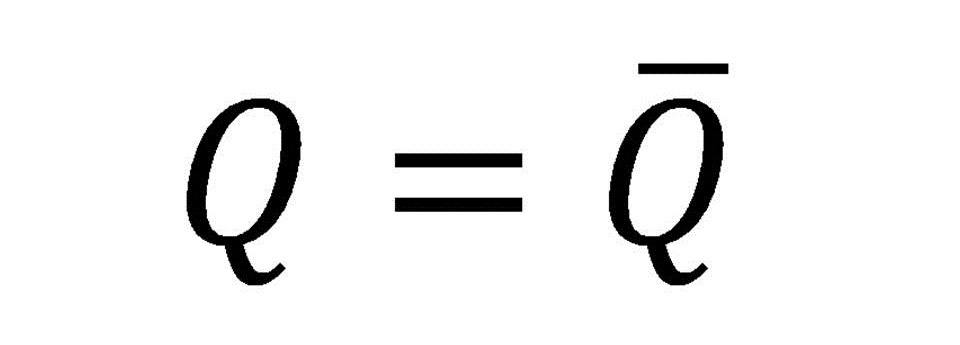
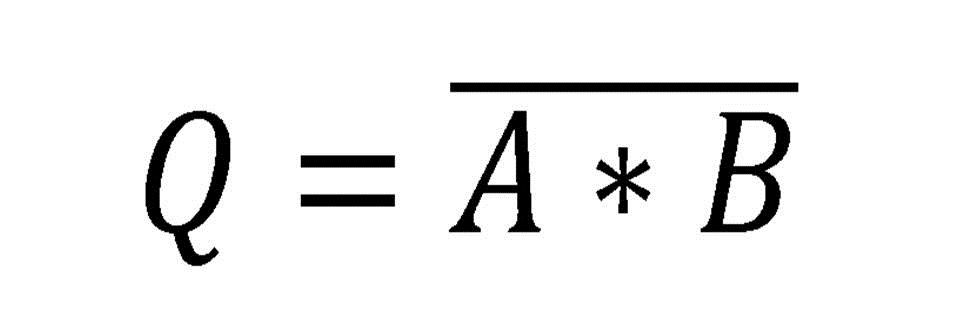


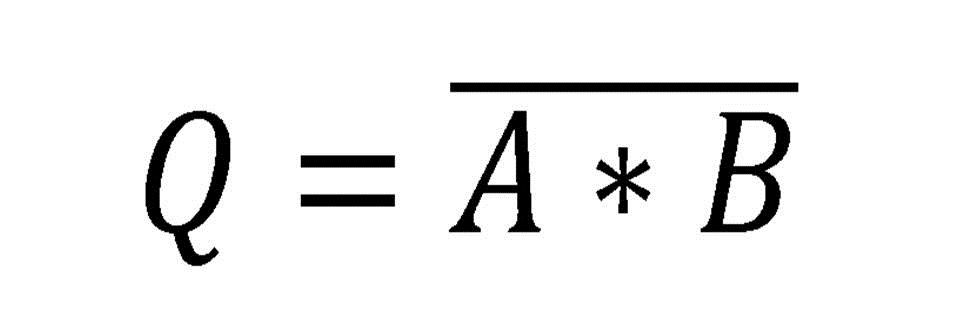

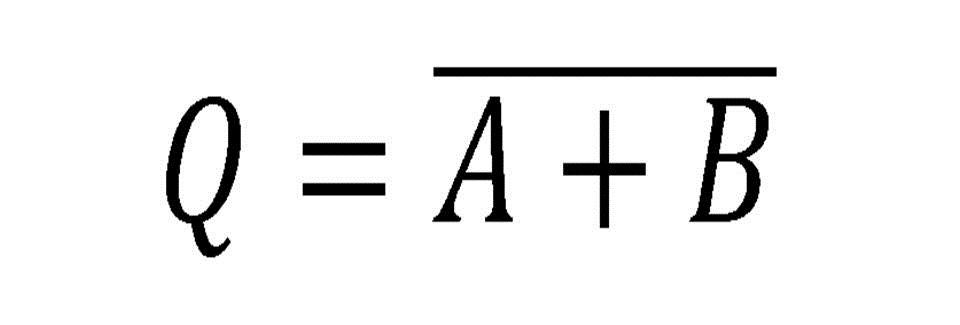


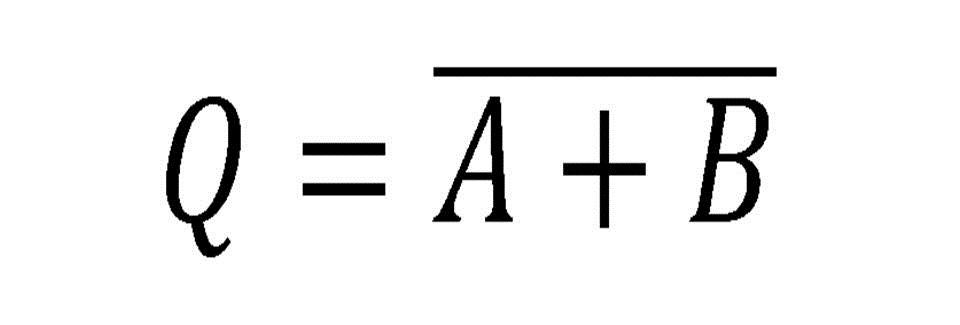

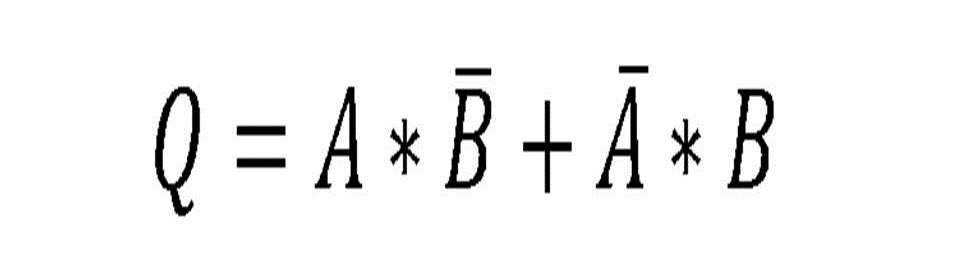


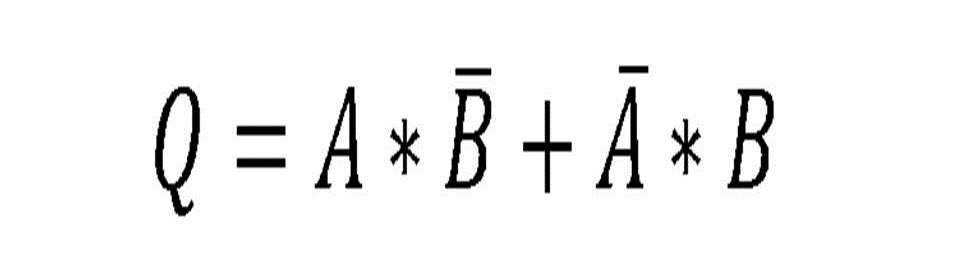

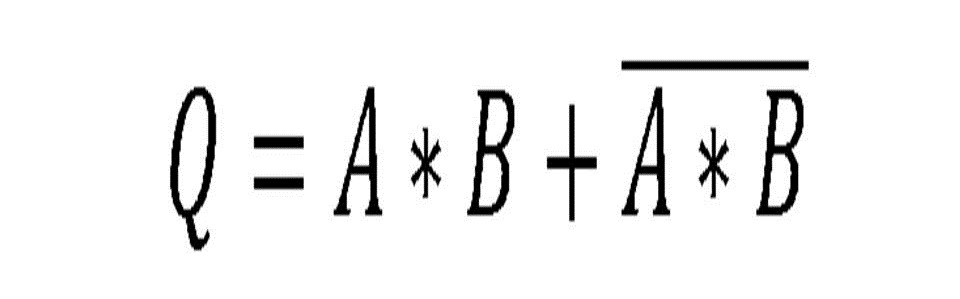







Buen contenido, me ayudas bastante gracias
ResponderBorrar