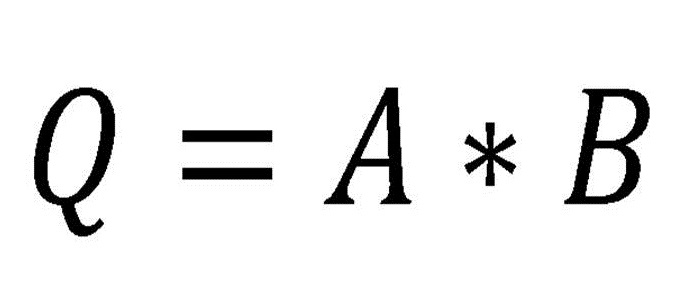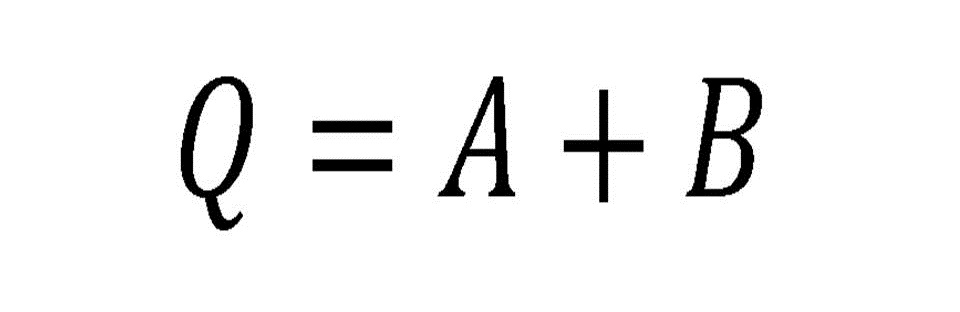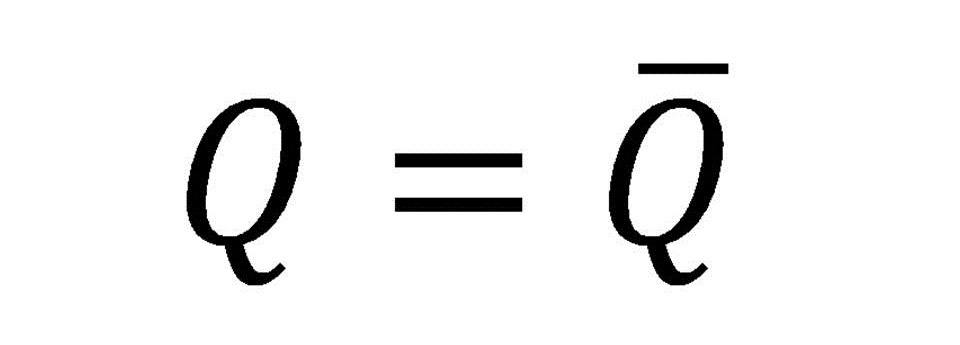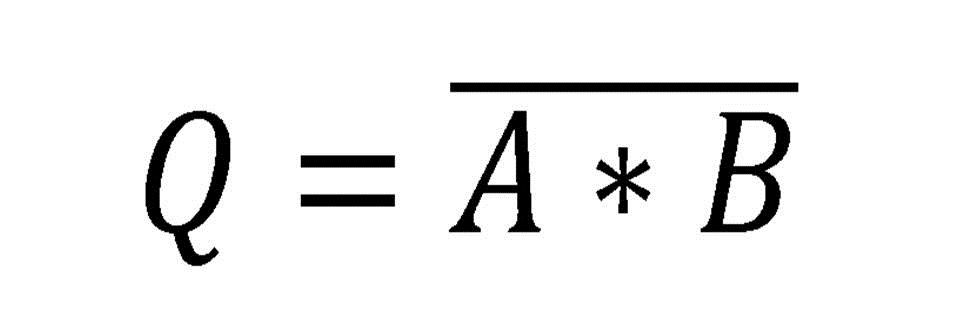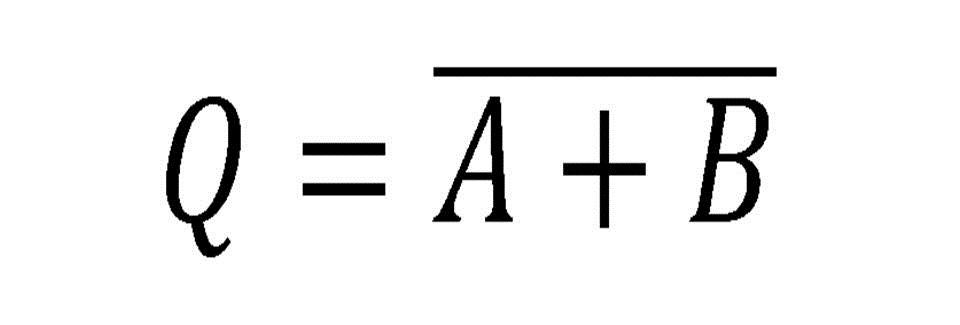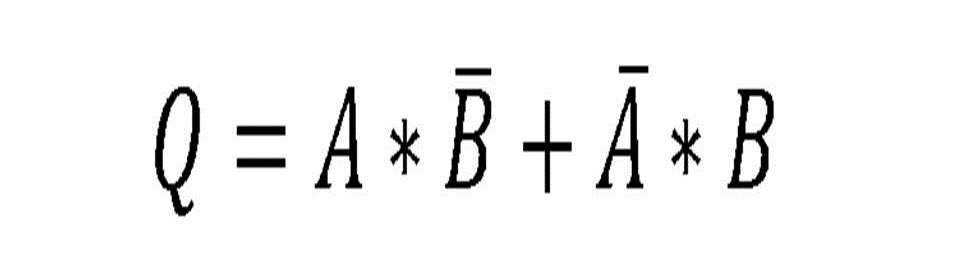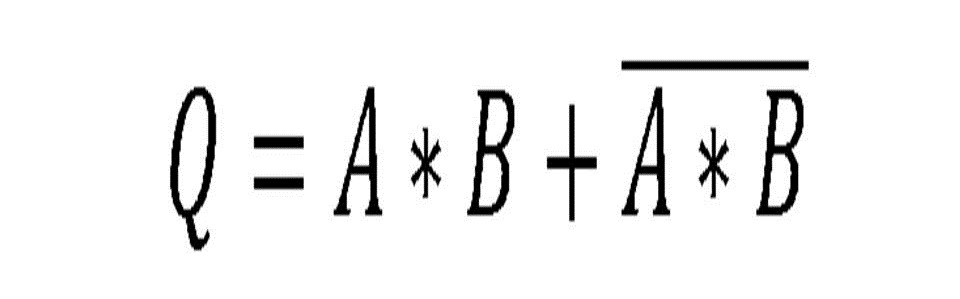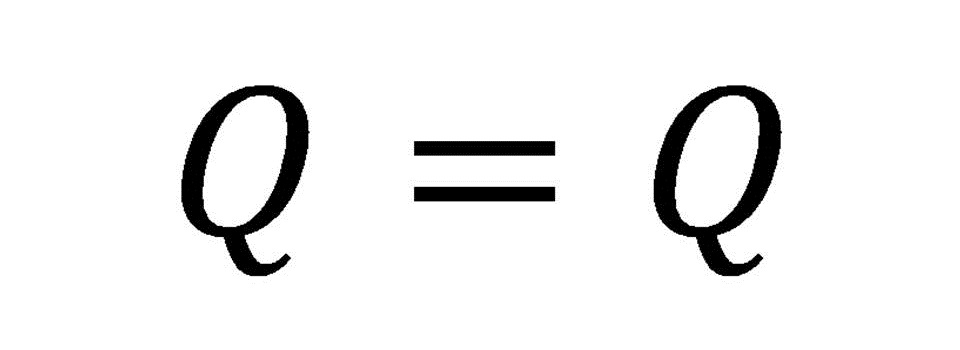Postulados del álgebra de Boole
Vamos a exponer los postulados más significativos,
y, para su mejor comprensión, acompañaremos cada uno de ellos con un circuito
eléctrico realizado mediante contactos. En la siguiente Figura aparece una
relación de la mayor parte de los postulados que veremos a continuación:
• Postulado 1
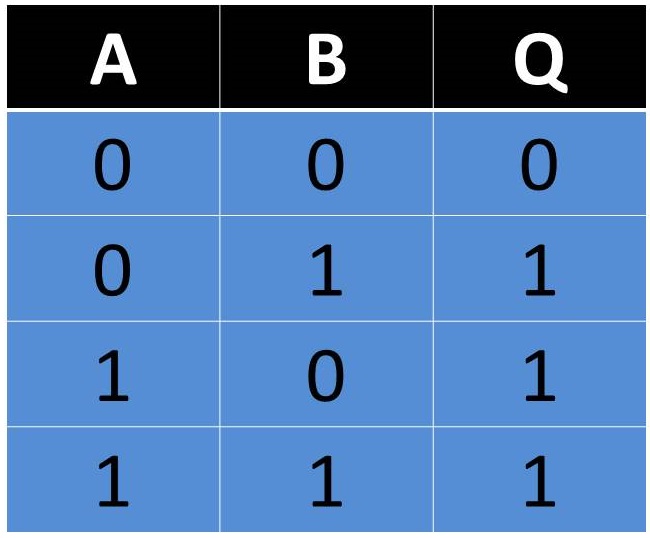
La suma lógica de una variable más un 1 lógico
equivale a un 1 lógico:
a + 1 = 1
Circuito eléctrico
equivalente de los postulados más significativos.
• Postulado 2
La suma lógica de una variable más un 0 lógico
equivale al valor de la variable:
a + 0 = a
• Postulado 3
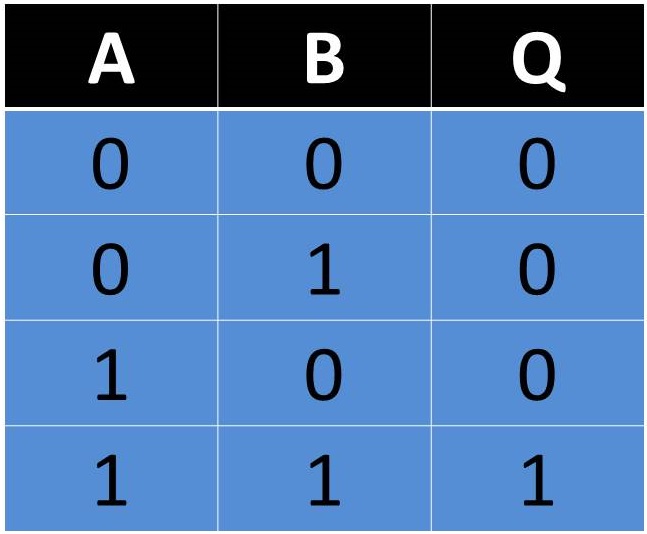
El producto lógico de una variable por un 1 lógico
es igual al valor de la variable:
a · l = a
• Postulado 4
El producto lógico de una variable por un 0 lógico
es igual a 0:
a · 0 = 0
• Postulado 5
La suma lógica de dos variables iguales equivale al
valor de dicha variable:
a + a = a
• Postulado 6
El producto lógico de dos variables iguales
equivale al valor de dicha variable:
a · a = a
• Postulado 7
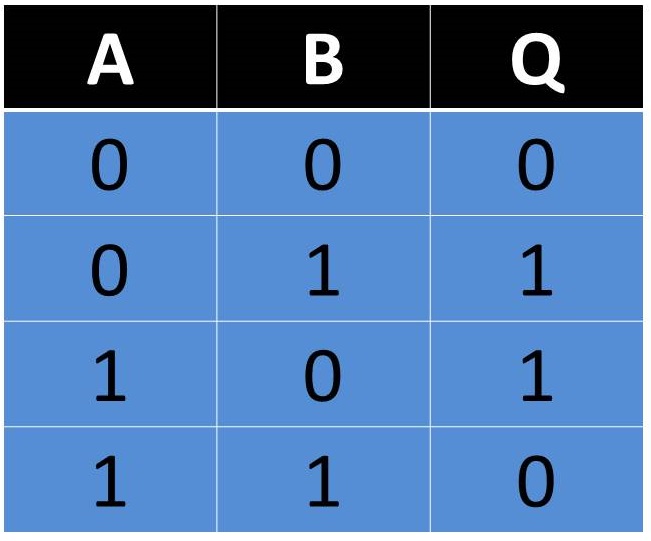
La suma lógica de una variable más la misma
variable negada equivale a un 1 lógico:
• Postulado 8
El producto lógico de una variable por la misma
variable negada equivale a un 0 lógico:
• Postulado 9
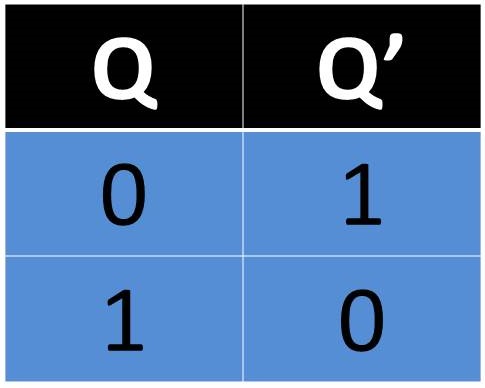
Si una variable es negada dos veces, ésta no varía.
Este postulado es válido para cualquier número par de inversiones:
• Otros postulados
Si se invierten los dos miembros de una igualdad,
ésta no sufre ninguna variación:
Propiedades
De la misma forma que en el sistema convencional,
en el álgebra de Boole se cumplen las
propiedades que describimos a continuación:
• Propiedad conmutativa:
a + b = b + a
a · b = b · a
• Propiedad asociativa:
a + b + e = a + (b + c)
a · b · c = a · (b · c)
• Propiedad distributiva:
a · (b + c) = a · b + a · c
a + b · c = (a + b) · (a + c)
Teoremas
Los teoremas que enunciamos seguidamente podrán ser
demostrados apoyándonos en los postulados y propiedades descritos
anteriormente.
• Teorema 1. Ley de absorción.
a) a + a · b = a
Demostración:
a + a · b = a · ( 1 + b ) = a · 1 = a
b) a · ( a + b) = a
Demostración:
a · (a + b) = a · a + a · b = a + a · b = a
Teorema 2.
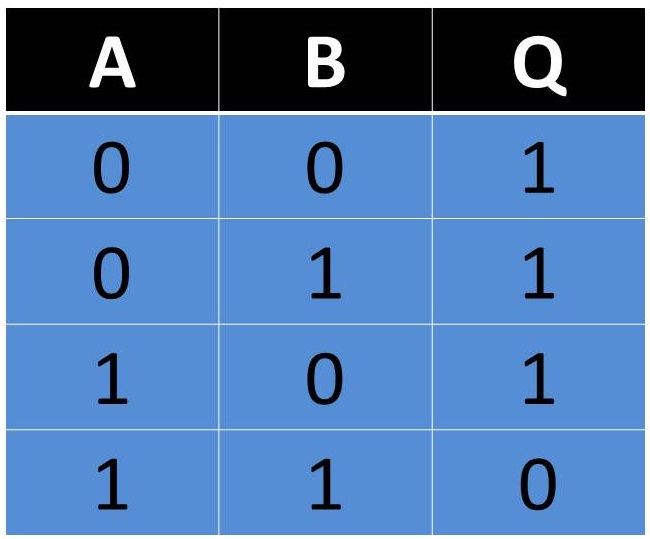
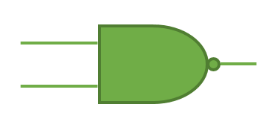
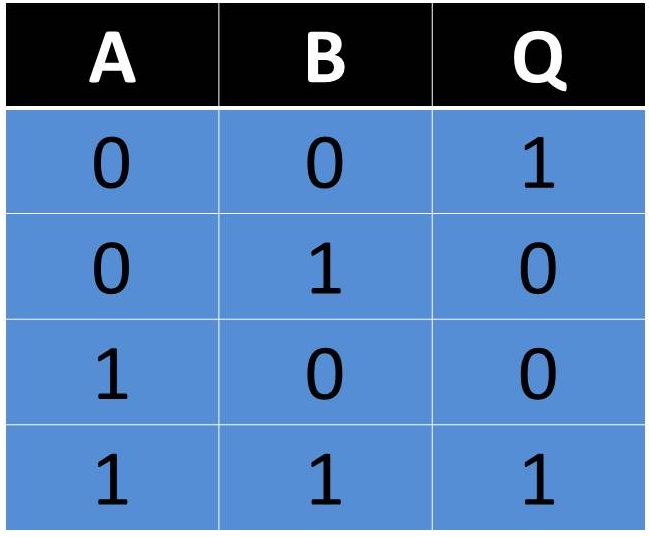
• Teorema 3. Leyes de De Morgan.
Merecen especial mención las leyes de De Morgan por
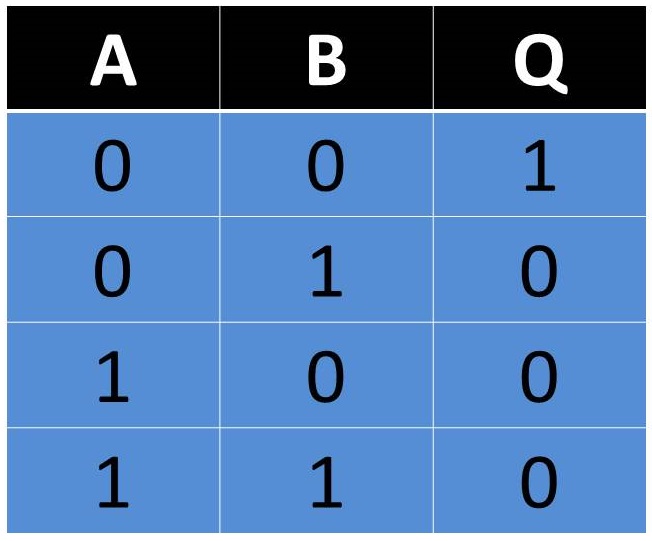
su gran utilidad en los procesos de simplificación. La comprobación de estos
teoremas la podrá realizar el(la) lector(a) construyendo la tabla de la verdad: